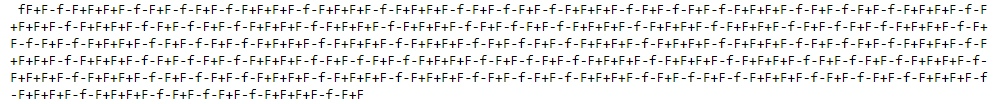Давайте начнём с азов, если брать определение из всем известной и всеми любимой Википедии, то L-система (или же система Линденмайера) — это параллельная система переписывания и вид формальной грамматики.
Если говорить простым языком, то L-система состоит из алфавита символов, которые могут быть использованы для создания строк, набора порождающих правил, которые задают правила подстановки вместо каждого символа, начальной строки ( “аксиомы” ), с которой начинается построение, и механизм перевода образованной строки в геометрические структуры. Самым простым примером L-системы может служить задача построения дерева.
Вводные данные:
Строка (далее Аксиома): A B
Переменные (которые мы можем задействовать в построении дерева): A B C
Правило (правило по которому каждая переменная на последующие строке меняется):
-
A — > AB
-
B — > AC
-
C — > A
Получаются такие преобразования:
|
Поколение |
Состояние |
|---|---|
|
1 |
A B |
|
2 |
AB AC |
|
3 |
AB AC AB A |
|
4 |
AB AC AB A AB AC AB |
|
5 |
AB AC AB A AB AC AB AB AC AB A AB AC |
|
6 |
и так далее… |
Основным направлением, в котором применяются L-системы, это моделирование процессов роста как живых организмов, так и неживых объектов (кристаллов, раковин моллюсков или пчелиных сот).
Пример:
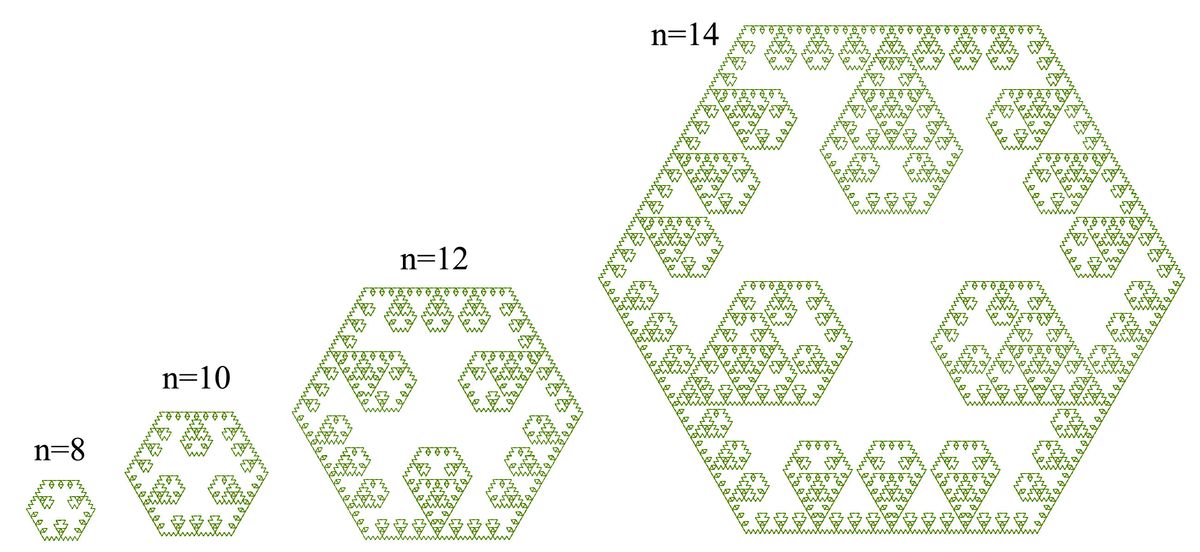
Для моделирования подобных процессов, мы с вами будем использовать такой язык программирования как Python, в нём есть встроенная библиотека “turtle”.

Итак, приступим:
-
Здесь мы импортируем библиотеку Turtle в наш проект:
import turtle -
Далее мы подключаем все необходимые конфигурации для нашей черепашки:
turtle.hideturtle()turtle.tracer(1)turtle.penup()turtle.setposition(-300,340)turtle.pendown()turtle.pensize(1) -
Далее мы задаём значение непосредственно самой аксиомы и сопутствующих параметров, необходимых для задания последовательности:
axiom = "F+F+F+F"tempAx = ""itr = 3(itr- значения итераций цикла, оно нам понадобится в следующем шаге при написании нашей программы)
-
В данном цикле, где как раз нам и понадобится переменная itr-, мы занимаемся обработкой и «выращиванием» непосредственно генома нашего фрактала/растения:
for k in range(itr):for ch in axiom:if ch == "+":tempAx = tempAx + "+"elif ch == "-":tempAx = tempAx + "-"elif ch == "F": #FtempAx = tempAx + "F+F-f-F+F"else:tempAx = tempAx + "f"axiom = tempAxtempAx = " "print(axiom)Если мы с вами пробежимся по циклу, то сразу же в первом условии мы увидим фильтр на символ «+»:
if ch == "+":tempAx = tempAx + "+"Здесь мы ищем в аксиоме (изначальной строке) знак “+” и при его появлении мы добавляем символ “+” в последующую строчку. Так же происходит и с символом “-” и “f”, мы просто добавляем в последующую строчку символы “-” и “f” соответственно. Но при появлении в нашей аксиоме символа “F”, мы поступим немного иначе и добавим в последующую строчку уже последовательность символов “F + F – f – F + F”, для увеличения длины каждой последующей строки. Данное действие в принципе не принципиально, но для быстроты генерации “генома”, я решил поступить именно так. В конце мы обязательно приравниваем аксиому к нашему геному и обнуляем его:
axiom = tempAxtempAx = " "Результат (значение аксиомы):
-
Ну что, вроде по генерации генома всё понятно, давайте уже приступим непосредственно к визуализации. Для этого нам понадобиться простенький цикл, который будет переводить встречающиеся в геноме символы в движения черепашки:
for ch in axiom:if ch == "+":turtle.right(45)turtle.forward(10)turtle.right(45)elif ch == "-":turtle.left(45)turtle.forward(10)turtle.left(45)else:turtle.forward(20)Сразу можно заметить, что по аналогии с предыдущим пунктом, мы детектируем символы «+», «-«, «F» и «f». Только теперь в момент, когда мы встречаем символ «+»:
if ch == "+":turtle.right(45)turtle.forward(10)turtle.right(45)Мы поворачиваем сначала на право, на 45 градусов, потом проезжаем расстояние, равное 10, и потом мы снова поворачиваем на право, на 45 градусов. Когда же мы встречаем символ «-«:
elif ch == "-":turtle.left(45)turtle.forward(10)turtle.left(45)Мы делаем все те же самые действия, что и при символе «+», только на этот раз поворачиваем уже не вправо, а уже влево. Но если же мы встретим символы «F» или «f», то мы просто буем проезжать вперёд на 20 пикселей:
else:turtle.forward(20)В итоге мы получаем вот такой фрактал-снежинку:
-
Если же мы захотим раскрасить наш фрактал-снежинку, то нам понадобиться перед циклом из предыдущего пункта добавить строчки:
turtle.fillcolor("#99BBFF")turtle.begin_fill()Где #99BBFF — это кодировка цвета (RGB: 153, 187, 255), а begin_fill() это начало заполнения цветом. И в конце, уже после цикла, добавить строчки:
turtle.end_fill()turtle.update()turtle.done()А end_fill() означает конец заполнения. Далее мы обновляем и выключаем нашу «черепашку». И на выходе мы получаем вот такой фрактал-снежинку:
Вы так же можете посмотреть, «потыкать» код, изменяя параметры и данные в нём.
В конце, хочу также добавить, что мне очень понравилось работать и писать по данной тематике, возможно, в будущем, я напишу ещё ряд статей по теме «L-системы», но а пока, хочу представить вам результаты моего тыканья творчества:


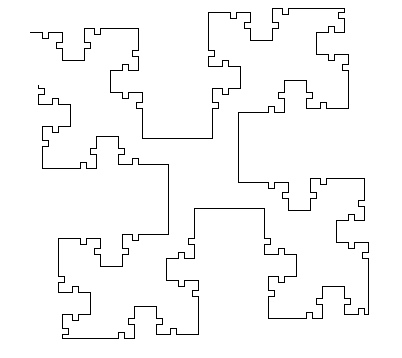

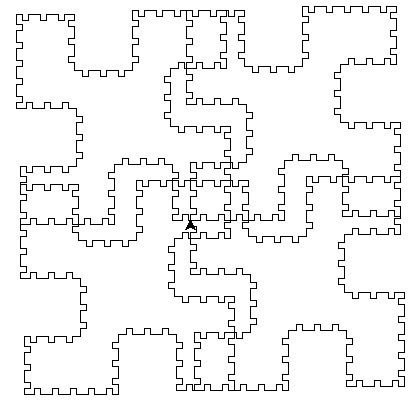
Автор: VolinNilov